Imagina que estás sentado tranquilamente en una silla o de pie sobre el suelo. Aunque no lo pienses, se está produciendo una fuerza para que no te caigas ni atravieses el suelo o la silla.
¿Te has preguntado alguna vez por qué, cuando dejas un objeto sobre una mesa, este no lo atraviesa y se cae al suelo? Aquí es donde entra en juego una fuerza "especial" en nuestra vida diaria: la fuerza normal.
En física, esta es una de las fuerzas más comunes y esenciales, pero a menudo pasa desapercibida. No tiene un nombre muy llamativo, pero sin ella, nuestras experiencias cotidianas serían muy diferentes.
A continuación te explicaré qué es exactamente esta fuerza, cómo actúa y por qué es tan importante para que las cosas, incluidos nosotros, permanezcan en su sitio.
¿Qué es la fuerza normal?
Definición
La fuerza normal es la fuerza de contacto que una superficie ejerce sobre un objeto cuando este está apoyado en ella. Esta fuerza se genera como reacción a otras fuerzas que actúan sobre el objeto, como su peso debido a la gravedad, y es responsable de que el objeto no atraviese la superficie ni se hunda en ella.
En resumen, esta fuerza es la respuesta de la superficie que contrarresta las fuerzas aplicadas sobre el objeto, manteniéndolo en equilibrio.
Explicación gráfica
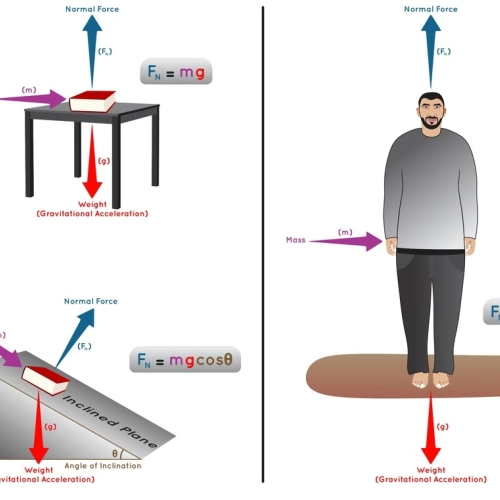Imaginad que estáis de pie sobre el suelo o sentados en una silla. En ambos casos, estáis apoyados sobre una superficie, ¿verdad?
Pues esa superficie está haciendo algo que a simple vista no notamos: está empujando contra nosotros hacia arriba para mantenernos en equilibrio. Ese empujón hacia arriba es lo que llamamos fuerza normal.
Es una fuerza que actúa perpendicularmente (en ángulo recto) a la superficie sobre la que un objeto está apoyado. Esta fuerza es como la respuesta de la superficie al peso del objeto que tiene encima. Y lo mismo pasa si dejamos un libro sobre una mesa o si apoyamos la mano sobre una pared.
Unidades
La fuerza normal, como cualquier otra fuerza, se mide en Newton (N).
Un Newton es la unidad de medida estándar de la fuerza en el Sistema Internacional de Unidades (SI), y se define como la fuerza necesaria para acelerar una masa de 1 kilogramo a una velocidad de 1 metro por segundo cuadrado.
Un ejemplo sencillo
Voy a poneros un ejemplo que os va a sonar: imaginaos que estáis en un parque, os sentáis en un banco, y notáis cómo el banco os sostiene sin que os caigáis al suelo. ¿Qué está pasando?
El banco está ejerciendo una fuerza hacia arriba, que es la fuerza normal, para contrarrestar la fuerza hacia abajo que hace la gravedad sobre vosotros, es decir, vuestro peso.
Entonces, cuando estáis sentados, hay dos fuerzas principales en juego:
- Vuestro peso, que es la fuerza que la gravedad ejerce hacia abajo.
- La fuerza normal, que es la respuesta del banco que empuja hacia arriba.
Esas dos fuerzas se compensan y por eso no os caéis al suelo ni atravesáis el banco. Así que, básicamente, ¡la fuerza normal es la responsable de que no nos hundamos en las cosas!
¿Por qué se llama "normal"?
La palabra "normal" en este caso no tiene nada que ver con lo que usamos en el día a día (como cuando decimos "eso es normal" o "esto es raro"). Aquí, "normal" significa perpendicular.
Es un término matemático que usamos en física para referirnos a una dirección específica, la que forma un ángulo de 90 grados con una superficie.
Así que cuando decimos "fuerza normal", estamos hablando de una fuerza que siempre apunta en esa dirección, hacia afuera y perpendicular a la superficie.
¿Cómo funciona exactamente?
Ahora que entendemos lo básico, vamos a profundizar un poco más en cómo funciona la fuerza normal. Esta fuerza no tiene un valor fijo. No es que siempre empuje hacia arriba con la misma intensidad. Su valor depende de varios factores, y uno de los más importantes es el peso del objeto.
Imagina que dejas caer un libro sobre una mesa. La fuerza que hace el libro sobre la mesa es el peso del libro, que es la fuerza de gravedad tirando hacia abajo. En respuesta, la mesa ejerce una fuerza hacia arriba, igual en magnitud al peso.
Si el libro pesa 2 kilogramos, la mesa empujará con una fuerza hacia arriba equivalente al peso del libro. Pero si añades más libros encima, la fuerza que ejerce la mesa (normal) tendrá que aumentar para seguir aguantando el peso extra.
Hay que tener en cuenta, que si además del peso existen otras fuerzas, estas también intervienen en la fuerza normal. Por ejemplo, si empujamos el libro con la mano hacia abajo, la fuerza normal será la suma del peso más la fuerja que ejercemos nosotros hacia abajo.
Cálculo de la fuerza normal con fórmulas
Distinguimos dos casos especiales: cuando el objeto está sobre una superfície horizontal y cuando está sobre un plano inclinado.
Càlculo en una superfície horizontal
La fórmula básica para calcular la fuerza normal, en situaciones donde el objeto está sobre una superficie horizontal sin inclinaciones ni fuerzas extras, es bastante sencilla:
Fn=m⋅g
Donde:
- m es la masa del objeto en kilogramos (kg).
- g es la aceleración de la gravedad, que en la Tierra es aproximadamente 9.8 m/s2.
Por ejemplo, si tienes un objeto que pesa 10 kg, su peso sería:
Peso=10 kg⋅9.8 m/s2=98N
Y la fuerza normal sería también de 98 Newtons (N), porque la superficie tiene que hacer una fuerza igual y opuesta para sostener el objeto en equilibrio.
Cálculo en un plano inclinado
Ahora vamos a ver cómo se calcula cuando un objeto está en un plano inclinado. Esto es un poco más complicado que en una superficie plana, porque no toda la fuerza del peso del objeto actúa directamente contra la superficie, ya que parte de esa fuerza está "deslizándose" hacia abajo a lo largo de la pendiente.
Cuando colocas un objeto sobre una superficie inclinada (como una rampa o una colina), su peso sigue actuando hacia abajo debido a la gravedad, pero se descompone en dos componentes:
- Un componente paralelo a la superficie inclinada: es la parte del peso que "empuja" al objeto hacia abajo a lo largo de la pendiente, y por eso los objetos pueden deslizarse en una rampa.
- Un componente perpendicular a la superficie inclinada: es la parte del peso que "presiona" directamente contra la rampa, y este es el que genera la fuerza normal.
Veamos cómo se calcula en este caso.
Descomposición del peso en un plano inclinado
Para calcular la fuerza normal en un plano inclinado, lo primero que tenemos que hacer es descomponer la fuerza de la gravedad en estas dos partes que mencioné antes: una paralela y otra perpendicular.
Si el ángulo de inclinación de la rampa es θ (el ángulo entre la superficie inclinada y el suelo plano), podemos usar trigonometría para calcular cada una de esas componentes.
El peso total del objeto es:
Peso=m⋅g
Donde m es la masa del objeto y g es la aceleración debida a la gravedad (aproximadamente 9.8 m/s2).
- Componente perpendicular (que es la que genera la fuerza normal):
Esta es la parte que nos interesa, porque es la que se "apoya" en la rampa y que está relacionada con la fuerza normal. La fórmula para calcular esta componente es:
F⊥=m⋅g⋅cos(θ)
Aquí, cos(θ) es el coseno del ángulo de inclinación. - Componente paralela (que hace que el objeto tienda a deslizarse):
No afecta directamente a la fuerza normal, pero es útil saberlo para entender el movimiento del objeto sobre la rampa. Se calcula así:
F∥=m⋅g⋅sin(θ)
Cálculo de la fuerza normal
Una vez que hemos descompuesto el peso en estas dos partes, ya podemos calcular la fuerza normal (Fn). La Fn en un plano inclinado será igual a la componente perpendicular de la fuerza de gravedad, ya que es esta la que la superficie de la rampa tiene que contrarrestar.
Por lo tanto, la fuerza normal es:
Fn=m⋅g⋅cos(θ)
Ejemplo práctico
Imagina que tienes un bloque de 5 kg colocado sobre una rampa inclinada a 30 grados respecto al suelo. Queremos calcular la fuerza normal que ejerce la rampa sobre el bloque.
Primero, calculamos el peso del bloque:
Peso=5 kg⋅9.8 m/s2=49 N
Ahora usamos la fórmula, con el ángulo de inclinación de 30 grados:
Fnormal=49 N⋅cos(30∘)
El coseno de 30 grados es aproximadamente 0.866, así que:
Fnormal=49 N⋅0.866=42.4 N
Por lo tanto, la fuerza normal que la rampa ejerce sobre el bloque es de 42.4 Newtons.
¿Por qué es más pequeña que en una superficie plana?
Fíjate que la fuerza normal en una rampa inclinada es menor que si el mismo bloque estuviera en una superficie plana. Si el bloque estuviera en una superficie horizontal (donde el ángulo θ es 0 grados), el coseno de 0 es 1, así que la fuerza normal sería igual al peso completo, es decir, 49 N.
En el caso de la rampa, como el ángulo de inclinación es de 30 grados, solo una parte del peso está siendo "apoyada" sobre la rampa, y por eso la fuerza normal es menor, 42.4 N en lugar de los 49 N que tendríamos en una superficie plana.
La otra componente de la fuerza es la que provocaría una aceleración del cuerpo hacia abajo a menos que existiera una fuerza de rozamiento en sentido contrario que la compensara.
Esto también explica por qué es más fácil que un objeto se deslice en una pendiente inclinada: como la fuerza normal es menor, hay menos fricción, y la parte del peso que actúa hacia abajo por la pendiente (la componente paralela) ayuda al objeto a moverse.
Situaciones especiales
Hasta ahora hemos hablado de ejemplos muy sencillos, pero esta fuerza también puede comportarse de maneras interesantes en situaciones más complejas.
A continuación te planteo algunos ejemplos especiales que te ayudaran a entender mejor este concepto:
1. Pendientes
Imaginaos que vais caminando por una colina inclinada. ¿Os habéis dado cuenta de que es más fácil resbalarse en una pendiente? Esto tiene que ver con la fuerza normal.
Cuando un objeto está sobre una superficie inclinada, la fuerza normal no es tan grande como cuando la superficie es plana, porque la inclinación hace que parte de la fuerza gravitatoria esté actuando "empujando" hacia abajo por la pendiente.
En una colina, la fuerza normal no tiene que compensar todo el peso del objeto, solo una parte. Y como es menor, hay menos resistencia y es más fácil que resbaléis.
2. Empujando contra una pared
Ahora, imaginaos que estáis empujando una caja contra una pared.
En este caso, la fuerza normal no está relacionada con el peso de la caja, sino con la presión que estáis ejerciendo. Cuanto más fuerte empujéis la caja contra la pared, mayor será la fuerza que la pared ejercerá hacia la caja para evitar que la atraviese.
Si dejáis de empujar, la fuerza normal desaparece.
3. Fuerza normal en un ascensor
¿Alguna vez habéis sentido que pesáis más o menos en un ascensor en movimiento?
Esto también tiene que ver con este tipo de fuerza. Si el ascensor sube de manera acelerada, la fuerza normal se incrementa (y sentimos como si pesáramos más), porque el suelo del ascensor tiene que empujar con más fuerza hacia arriba para compensar la aceleración.
Si el ascensor baja acelerando, la fuerza normal disminuye (y sentimos que pesamos menos), porque la aceleración reduce la necesidad de empujar hacia arriba con tanta fuerza.
Relación con la tercera ley de Newton: acción y reacción
La fuerza normal está directamente relacionada con la tercera ley de Newton, también conocida como la ley de acción y reacción.
Esta ley dice que por cada acción, existe una reacción de igual magnitud y en sentido opuesto. Es decir, si un objeto ejerce una fuerza sobre otro, ese otro objeto responde con una fuerza igual pero en la dirección contraria.
En el caso de la fuerza normal, imagina una patinadora deslizándose encima de una pista de hielo. El peso de la patinadora, que es la fuerza de acción, empuja hacia abajo debido a la gravedad.
Como reacción, el hielo ejerce una fuerza hacia arriba para contrarrestar ese peso y evitar que se rompa y la patinadora lo atraviese. La magnitud de esta fuerza es igual al peso de la patinadora, pero actúa en dirección opuesta, es decir, hacia arriba.
Conclusión
En resumen, la fuerza normal es una de esas cosas que está presente todo el tiempo, pero que normalmente no nos damos cuenta de que existe.
Es la fuerza que evita que atravesemos el suelo o que los objetos se hundan en las superficies. Depende del peso del objeto y siempre actúa perpendicular a la superficie en la que está apoyado. Además, está involucrada en todo tipo de situaciones cotidianas, desde estar sentados hasta caminar por una pendiente.