El movimiento circular uniforme (MCU) es un concepto fundamental en cinemática que describe un tipo específico de movimiento en el que un objeto se desplaza alrededor de un punto fijo en una trayectoria circular a una velocidad constante.
En este artículo, definiremos el MCU, y los diferentes conceptos básicos relacionados con este movimiento, algunos ejemplos reales que ilustren este movimiento, las fórmulas para su cálculo y resolveremos algunos ejercicios para comprenderlo mejor.
Definición del movimiento circular uniforme (MCU)
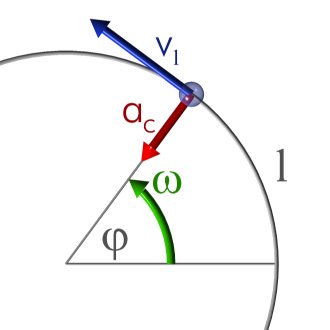El movimiento circular uniforme (MCU) es un tipo específico de movimiento en el que un objeto se desplaza alrededor de un punto fijo en una trayectoria circular a una velocidad constante.
En el MCU, la velocidad del objeto se mantiene invariable en magnitud y dirección a lo largo de su recorrido, lo que significa que la velocidad angular es constante.
El movimiento circular uniforme se caracteriza por la relación entre la velocidad angular y la velocidad lineal, que está directamente relacionada con el radio de la trayectoria circular.
Este movimiento es típicamente observado en situaciones como la órbita de un planeta alrededor de una estrella, el giro de una rueda en un vehículo en movimiento, o incluso en parques de atracciones en las montañas rusas, donde los pasajeros experimentan una sensación constante de velocidad y dirección a medida que giran alrededor de un punto central.
Conceptos básicos del MCU
Para comprender el MCU, es fundamental familiarizarse con algunos conceptos clave:
1. Periodo (T) y frecuencia (f)
El período (T) es el tiempo que toma para que el objeto complete una vuelta completa alrededor de la trayectoria circular. La frecuencia (f) es la cantidad de vueltas que el objeto completa en un segundo. Están relacionados de la siguiente manera:
f = 1 / T
En el Sistema Internacional de Unidades (SI), el período se mide en segundos (s). Por otro lado, la frecuencia se mide en hertz (Hz). Un hertz es igual a un ciclo por segundo.
2. Velocidad angular (ω)
La velocidad angular (ω) es una medida de la rapidez con la que el objeto se desplaza alrededor de la trayectoria circular. Se mide en radianes por segundo (rad/s) y está relacionada con la frecuencia (f) de la siguiente manera:
ω = 2·π·f
3. Radio de la trayectoria (r)
El radio de la trayectoria (r) es la distancia desde el punto central al objeto que se mueve en el MCU. Este valor es constante durante todo el movimiento.
4. Velocidad lineal (v)
La velocidad lineal (v) es la rapidez con la que el objeto se mueve tangencialmente a lo largo de la trayectoria circular. Por esta razón también se conoce como velocidad tangencial.
La velocidad tangencial está relacionada con la velocidad angular (ω) y el radio (r) de la siguiente manera:
v = r·ω
5. Aceleración centrípeta (ac)
La aceleración centrípeta (ac) es una aceleración ficticia que actúa sobre el objeto en dirección opuesta al centro de la trayectoria circular. Su magnitud está relacionada con la velocidad angular (ω) y el radio (r) de la siguiente manera:
ac=r·ω2
Las unidades de la aceleración centrípeta son metros por segundo al cuadrado (m/s²).
Fórmulas del movimiento circular uniforme
Las siguientes fórmulas son esenciales para comprender y resolver problemas relacionados con el MCU:
-
Relación entre la velocidad angular y la velocidad lineal: v=rω
-
Relación entre el período y la frecuencia:T=1/f
-
Relación entre la velocidad angular y la frecuencia: ω=2πf
-
Relación entre la aceleración centrípeta, la velocidad angular y el radio: ac=rω2
Ejemplos en la vida cotidiana
El movimiento circular uniforme se encuentra en numerosos aspectos de la vida cotidiana.
-
Turbinas de vapor en centrales nucleares: Las turbinas de vapor en centrales nucleares emplean el MCU para convertir la energía térmica en energía mecánica, generando electricidad.
-
Ventiladores de techo: Las aspas de los ventiladores de techo realizan un MCU para circular el aire de manera uniforme en una habitación, proporcionando enfriamiento.
-
Los vehículos en curvas: los vehículos, al girar en curvas circulares, siguen un MCU que se puede calcular utilizando estas fórmulas.
-
Fabricación de cuerdas: Girar una cuerda para crear una soga implica un MCU, donde la cuerda se enrolla de manera uniforme alrededor de un núcleo central.
Ejercicios resueltos
Ahora, resolvamos algunos ejercicios típicos relacionados con el MCU:
Ejercicio 1
Supongamos que un coche de carreras se desplaza a una velocidad constante de 100 m/s alrededor de una pista circular de radio 200 metros. Calcula el período, la frecuencia y la velocidad angular del movimiento.
Solución:
Dado que la velocidad es constante, podemos utilizar la fórmula para la velocidad angular:
v = r·ω
Sustituyendo los valores conocidos:
100 m/s = 200 m ⋅ ω
Para encontrar ω:
ω = (100 m/s) / 200 m=0.5 rad/s
Ahora, podemos encontrar el período (T) utilizando la relación entre la velocidad angular y la frecuencia:
ω = 2·π·f
0.5 rad/s = 2·π⋅f
Para encontrar f:
f = (0.5 rad/s) / (2·π) ≈ 0.0796 Hz
Y, finalmente, el período (T) es el recíproco de la frecuencia:
T = 1/f ≈ 12.57 s
Ejercicio 2
Un objeto se desplaza a lo largo de una trayectoria circular de radio 4 metros a una velocidad angular de 2 radianes por segundo. Calcula su velocidad lineal y su aceleración centrípeta.
Solución:
Para encontrar la velocidad lineal, utilizamos la fórmula:
v = r·ω
Sustituyendo los valores conocidos:
v=4m ⋅ 2 rad/s = 8 m/s
Para la aceleración centrípeta, usamos la fórmula:
ac = r·ω2
Sustituyendo los valores conocidos:
ac=4 m⋅(2 rad/s)2=16 m/s2
