El movimiento circular uniformemente acelerado (MCUA) es un tipo de movimiento en el que un objeto se mueve a lo largo de una trayectoria circular con una aceleración constante.
El MCUA es un tipo de movimiento crucial en el cálculo de la cinemática de un cuerpo. Este fenómeno es fundamental para comprender una amplia gama de situaciones, desde la mecánica de vehículos hasta la dinámica de los planetas en órbita, y se puede describir mediante fórmulas específicas que relacionan la velocidad angular, la aceleración angular y el tiempo.
¿Qué es el movimiento circular uniformemente acelerado?
El movimiento circular uniformemente acelerado (MCUA) es un concepto fundamental en la física que describe el movimiento de un objeto a lo largo de una trayectoria circular con una aceleración constante.
A diferencia del movimiento rectilíneo, en el que un objeto se mueve en línea recta, el MCUA involucra una constante variación en la velocidad angular del objeto, lo que lo lleva a rotar a lo largo de una curva cerrada.
En el MCUA, la aceleración angular del objeto es constante, lo que significa que su velocidad angular aumenta o disminuye de manera uniforme con el tiempo.
Características básicas del movimiento
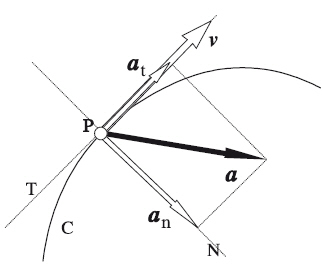Las características básicas que definen este movimiento son:
- El objeto se mueve describiendo una trayectoria circular. Esto implica la aparición de una aceleración centrípeta para mantener constante la distancia del objeto al centro de rotación.
- La velocidad angular sufre una aceleración angular constante, por lo tanto, la velocidad tangencial también sufre una aceleración tangencial.
Conceptos básicos
Velocidad angular
La velocidad angular, representada por la letra griega "ω" (omega), es una medida de la rapidez con la que un objeto gira a lo largo de la trayectoria circular. Se mide en radianes por segundo (rad/s).
Velocidad tangencial
La velocidad tangencial es la velocidad lineal de un objeto en un punto específico de su trayectoria circular. Se refiere a la magnitud de la velocidad de un objeto en una dirección tangente a la curva en ese punto.
Aceleración angular
La aceleración angular, representada por "α" (alfa), es el cambio en la velocidad angular por unidad de tiempo. Al igual que la velocidad angular, se mide en radianes por segundo al cuadrado (rad/s²).
Aceleración centrípeta
La aceleración centrípeta es una aceleración dirigida hacia el centro de una trayectoria circular. Se produce cuando un objeto se desplaza en una órbita curva y experimenta un cambio constante en la dirección de su velocidad sin afectar su magnitud.
Aceleración tangencial
La aceleración tangencial es una medida de cómo cambia la magnitud de la velocidad de un objeto en movimiento a lo largo de una trayectoria curva. Esta aceleración se produce cuando la velocidad tangencial del objeto varía.
Fórmulas de cálculo
Fórmula de la velocidad angular en función del tiempo
La relación entre la velocidad angular inicial (ω₀), la aceleración angular (α) y el tiempo (t) se puede describir mediante la siguiente fórmula:
ω= ω₀ + α·t
Dónde
- ω es la velocidad angular final.
- ω₀ es la velocidad angular inicial.
- α es la aceleración angular.
- t es el tiempo
Fórmula del ángulo rotado
La cantidad de ángulo rotado (θ) en un tiempo "t" está relacionada con la velocidad angular y la aceleración angular de la siguiente manera:
θ = ω₀·t + ½·α·t²
Dónde
- θ es el ángulo rotado.
- ω₀ es la velocidad angular inicial.
- α es la aceleración angular.
- t es el tiempo
Fórmula de la velocidad angular en función de la velocidad angular
La velocidad angular final (ω) se relaciona con la velocidad angular inicial, la aceleración angular y el ángulo rotado mediante la siguiente fórmula:
ω² = ω₀² + 2·α·θ
Dónde
- ω es la velocidad angular final.
- θ es el ángulo rotado.
- ω₀ es la velocidad angular inicial.
- α es la aceleración angular
Ejemplos cotidianos ilustrativos
El movimiento circular uniformemente acelerado (MCUA) se encuentra en numerosos aspectos de la vida cotidiana y en diversos contextos, algunos ejemplos incluyen:
- Lavadora de ropa: En el ciclo de centrifugado, la ropa gira en el tambor con una aceleración constante, permitiendo que el agua se expulse hacia afuera.
- Juegos de feria: Las atracciones de feria, como las norias y los carruseles, aplican un MCUA para arrancar y parar para permitir que los pasajeros puedan subir y bajar.
- Aerogeneradores: los molinos de viento sufren un MCUA cuando se ponen en marcha o cuando hay variaciones en la intensidad del viento.
- Turbinas de vapor: las turbinas de una central nuclear están optimizadas para girar a una velocidad constante. Mientras se produce el movimiento circular uniformemente acelerado durante el arranque y el paro, su eficiencia es menor.
Ejercicios resueltos
Ejercicio 1: Rotación de un ventilador
Un ventilador gira con una velocidad angular inicial de 3 rad/s y experimenta una aceleración angular de 0.5 rad/s². ¿Cuánto tiempo le llevará alcanzar una velocidad angular de 7 rad/s?
Solución
Utilizamos la fórmula para la velocidad angular final:
ω = ω₀ + αt
Sustituimos los valores conocidos:
7 rad/s = 3 rad/s + (0.5 rad/s²)·t
Resolvemos para t:
(0.5 rad/s²)t = 7rad/s − 3 rad/s
0.5t = 4 rad/s
t=(4 rad/s) / (0.5 rad/s²) = 8 s
El ventilador tomará 8 s para alcanzar una velocidad angular de 7 rad/s.
Ejercicio 2: Giro de una noria
Una noria comienza a girar desde el reposo con una aceleración angular de 0.8 rad/s². ¿Cuánto tiempo tomará para que la noria gire 5 radianes?
Solución
Utilizamos la fórmula para el ángulo rotado:
θ = ω₀t + ½·α·t²
Sustituimos los valores conocidos:
5rad = (0 rad/s)·t + ½(0.8 rad/s²)·t²
Simplificamos la ecuación:
5rad = (0.4 rad/s²)t²
Resolvemos para t:
t = √( 5 rad / 0.4 rad/s²)
t ≈ 3.54s
La noria tomará aproximadamente 3.54s para girar 5 radianes desde el reposo.