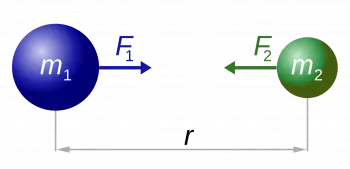
La Ley de la Gravitación Universal de Newton es uno de los pilares fundamentales de la física y fue desarrollada por Sir Isaac Newton en el siglo XVII. Esta ley describe la fuerza de atracción entre dos cuerpos debido a su masa y distancia relativa.
Es una de las leyes más importantes y ampliamente aplicadas en el campo de la física clásica y ha permitido comprender y predecir muchos fenómenos en el universo.
En este artículo, exploraremos en detalle qué es la Ley de la Gravitación Universal, su fórmula, su importancia y algunos ejemplos que ilustran su aplicación.
¿Qué es la Ley de la Gravitación Universal?
La Ley de la Gravitación Universal establece que la fuerza de atracción entre dos cuerpos es directamente proporcional al producto de sus masas e inversamente proporcional al cuadrado de la distancia que los separa.
Es decir, cuanto mayor sea la masa de los objetos y más cerca estén entre sí, mayor será la fuerza de atracción gravitacional entre ellos.
La fórmula de la Ley de la Gravitación Universal:
La fórmula matemática para calcular la fuerza gravitacional entre dos objetos se expresa de la siguiente manera:
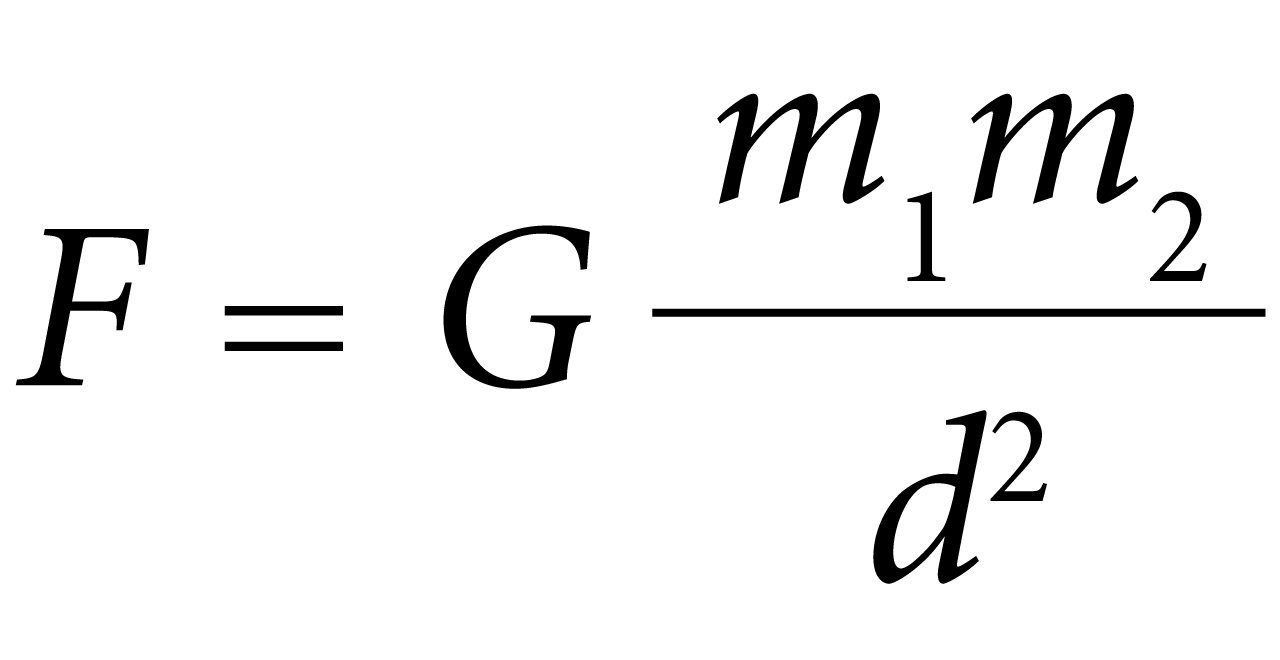
Donde:
-
F es la fuerza gravitacional entre los objetos expresada en newtons,
-
G es la constante de gravitación universal, aproximandamente 6.674 × 10-11 N (m/kg)2
-
m1 y m2 son las masas de los objetos expresada en quilogramos (kg).
-
r es la distancia entre los centros de masa de los objetos expresada en metros (m).
La constante de gravitación universal (G) tiene un valor de aproximadamente 6.674 × 10-11 N (m/kg)2 y se utiliza para escalar la fuerza de atracción en función de las unidades de masa y distancia utilizadas.
Importancia de la Ley de la Gravitación Universal:
La Ley de la Gravitación Universal es de suma importancia en el estudio y la comprensión del universo. A través de esta ley, podemos explicar y predecir fenómenos como la órbita de los planetas alrededor del Sol, los movimientos de las lunas alrededor de los planetas y la interacción entre objetos masivos en el espacio.
Además, la ley también tiene aplicaciones prácticas en la vida cotidiana. Por ejemplo, permite entender el funcionamiento de los satélites artificiales que orbitan alrededor de la Tierra y es esencial para la navegación espacial y la planificación de misiones espaciales.
Ejemplos de la aplicación de la Ley de la Gravitación Universal:
A continuación mostramos 4 ejemplos en los que se aplica la ley de la gravitación universal de Newton:
1. Órbita de la Tierra alrededor del Sol
La fuerza gravitacional entre la Tierra y el Sol es responsable de mantener a nuestro planeta en una órbita estable alrededor de la estrella.
Esta fuerza permite que la Tierra se mantenga en movimiento circular alrededor del Sol y determina el período de un año. La fuerza que ejerce el Sol sobre la Tierra es perpendicular a la velocidad lineal de la Tierra en cada momento.
2. La Luna y las mareas
La fuerza gravitacional entre la Tierra y la Luna es la responsable de las mareas. La Luna ejerce una fuerza de atracción sobre los océanos, lo que provoca el ascenso y descenso del nivel del agua a medida que la Tierra rota.
Al igual que sucede con el Sol y la Tierra, esta fuerza es la fuerza centrípeta que obliga a la Luna a orbitar alrededor de la Tierra.
3. Satélites artificiales
En el diseño y funcionamiento de los satélites artificiales también se realizan cálculas utilizando la fómrula de la ley de la gravitación universal.
Para mantener un satélite en órbita, se necesita una velocidad y altitud específicas que equilibren la fuerza gravitacional con la fuerza centrífuga generada por el movimiento orbital.
4. Caída de objetos
La ley también se aplica a la caída de objetos en la superficie de la Tierra. Cuanto mayor sea la masa del objeto, mayor será la fuerza gravitacional que actúa sobre él y más rápido caerá.
Ejercicios de la ley de la gravitación universal
A continuación mostramos tres ejercicios resueltos que ilustran la aplicación de esta ley de la física:
Ejercicio 1: Calculando la fuerza gravitacional entre dos cuerpos
Supongamos que tenemos dos objetos: uno con una masa de 5 kg y otro con una masa de 8 kg. La distancia entre los centros de masa de los objetos es de 2 metros. Queremos calcular la fuerza gravitacional entre ellos.
Datos
-
m1 = 5 kg
-
m2 = 8 kg
-
r = 2 m
-
G = 6.674 × 10-11 N (m/kg)2
Solución:
Utilizamos la fórmula de la Ley de la Gravitación Universal:
F = G (m1·m2) / r2
Sustituyendo los valores conocidos:
F = (6.674 × 10-11 N (m/kg)2) * (5 kg * 8 kg) / (2 m)2
F = 6,674 × 10-10 N
Por lo tanto, la fuerza gravitacional entre los dos cuerpos es aproximadamente de 6,674 × 10-10 N.
Ejercicio 2: Calculando la fuerza gravitacional entre la Tierra y un objeto
Supongamos que queremos calcular la fuerza gravitacional entre la Tierra (masa ≈ 5.972 × 1024 kg) y un objeto con una masa de 100 kg. La distancia entre el centro de la Tierra y el objeto es de 6.371 × 10^6 metros (radio aproximado de la Tierra).
Datos:
-
m1 (masa de la Tierra) = 5.972 × 1024 kg
-
m2 (masa del objeto) = 100 kg
-
r (distancia) = 6.371 × 106 m
-
G = 6.674 × 10-11 N (m/kg)2
Solución:
Aplicamos la fórmula de la Ley de la Gravitación Universal:
F = G (m1·m2) / r2
Sustituyendo los valores conocidos:
F = (6.674 × 10-11 N (m/kg) 2 ) * ((5.972 × 1024 kg) * (100 kg)) / (6.371 × 106 m)2
F = 981.95 N
Por lo tanto, la fuerza gravitacional entre la Tierra y el objeto es de aproximadamente 981.95 N.
Ejercicio 3: Calculando la masa de un objeto a partir de la fuerza gravitacional
Supongamos que tenemos dos objetos, y sabemos que la fuerza gravitacional entre ellos es de 100 N. La distancia entre los objetos es de 10 metros y la masa de uno de los objetos es de 5 kg. Queremos calcular la masa del segundo objeto.
Datos:
-
F = 100 N
-
r = 10 m
-
m1 = 5 kg
-
G = 6.674 × 10-11 N (m/kg)2
Solución:
Usamos la fórmula de la Ley de la Gravitación Universal y despejamos m2:
F = G (m1·m2) / r2
Despejamos m2:
m2 = (F * r2) / (G * m1)
Sustituyendo los valores conocidos:
m2 = (100 N * (10 m)2) / ((6.674 × 10-11 N (m/kg)2) * 5 kg)
m2 ≈ 2.997 × 1013 kg
Por lo tanto, la masa del segundo objeto es aproximadamente de 2.997 × 1013 kg.
