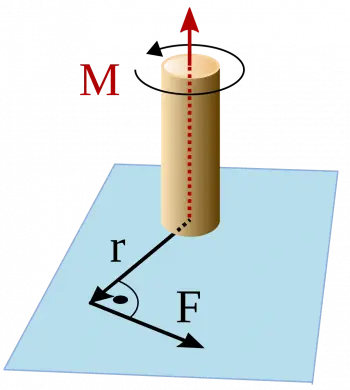
El momento de una fuerza, también conocido como "torque", es una magnitud física que mide la tendencia de una fuerza a girar un objeto alrededor de un punto o eje de rotación.
El momento de una fuerza está relacionado con las leyes de Newton porque la magnitud de la fuerza aplicada afecta a la aceleración angular del objeto (segunda ley) y porque el momento generado por la fuerza en un objeto también genera una fuerza igual pero opuesta en la dirección del eje de rotación o en otro objeto (tercera ley).
Matemáticamente, el momento de una fuerza se define como el producto del valor de la fuerza (F) y la distancia perpendicular (r) desde el punto de aplicación de la fuerza hasta el eje de rotación.
El momento de una fuerza se puede calcular en diferentes situaciones, ya sea en el contexto de un objeto en reposo (estática) o en movimiento (dinámica).
Fórmula del momento de una fuerza
La fórmula para calcular el momento (τ) de una fuerza (F) respecto a un punto o eje de rotación, tomando en cuenta la distancia perpendicular (r) desde el punto de aplicación de la fuerza al eje de rotación, es la siguiente:
Momento (τ) = F × r
Donde:
- τ = Momento de la fuerza (torque) en unidades de newton metro (Nm) o libra pie (lb-ft)
- F = Magnitud de la fuerza aplicada, medida en newtons (N) o libras (lb)
- r = Distancia perpendicular desde el punto de aplicación de la fuerza al eje de rotación, medida en metros (m) o pies (ft)
Esta fórmula se aplica cuando la fuerza y la distancia son perpendiculares entre sí, lo que significa que la fuerza actúa en una dirección que forma un ángulo de 90 grados con respecto al radio o distancia desde el eje de rotación.
En situaciones donde la fuerza y la distancia no son perpendiculares, es necesario utilizar conceptos de vectores o trigonometría para descomponer la fuerza en sus componentes perpendiculares al radio, lo que permitirá calcular el momento resultante.
Si se realiza en términos de vectores, la dirección del momento sigue la regla de la mano derecha o la regla del sacacorchos, según la convención. Esto implica que el momento puede ser positivo o negativo dependiendo de la dirección en la que actúe la fuerza en relación con el eje de rotación.
Ejemplos cotidianos
El momento de una fuerza tiene aplicaciones comunes en nuestra vida diaria en diversas situaciones. Aquí tienes algunos ejemplos de cómo se aplica el momento de una fuerza en el día a día:
- Abrir puertas: Cuando giras una manija de una puerta para abrirla, estás aplicando un momento sobre las bisagras. Cuanto más lejos esté la fuerza aplicada de las bisagras, más fácil será abrir la puerta, ya que aumentará el momento y requerirá menos fuerza para realizar el giro.
Polea: Una polea es una rueda con una cuerda o cable que la atraviesa. Al tirar de un extremo de la cuerda (fuerza de entrada), se aplica un momento sobre la polea, lo que permite levantar una carga en el otro extremo (fuerza de salida).- Apretar tornillos: Al usar una llave para apretar un tornillo, aplicas un momento alrededor del eje del tornillo. El largo de la llave (distancia desde el eje del tornillo) influye en la cantidad de fuerza que necesitas aplicar para apretar el tornillo con éxito.
- Girar una llave inglesa: Al usar una llave inglesa para aflojar o apretar tuercas y pernos, estás aplicando un momento alrededor del eje del perno. De nuevo, el largo de la llave inglesa determina la cantidad de momento que se genera y, por lo tanto, la facilidad para girar la tuerca o el perno.
- Volante de un automóvil: al girar el volante de un automóvil para cambiar la dirección, aplicas un momento sobre el eje de dirección del vehículo. Cuanto más lejos gires el volante del eje de dirección, más rápido cambiará la dirección del automóvil.
- Balanceo en un columpio: Cuando te columpias, aplicas un momento alrededor de los ganchos del columpio. Al empujar tus pies hacia adelante y hacia atrás mientras estás sentado en el columpio, controlas el momento y determinas la amplitud y la velocidad del movimiento.
- Bicicleta: al aplicar una fuerza a los pedales de una bicicleta genera un momento de fuerzas respecto al eje de los pedales. Así mismo, la fuerza que se transmite a la cadena depende directamente del radio de los platos, que es la distancia al centro de rotación.
- Palanca: Una palanca es una máquina simple que consta de una barra rígida que pivota alrededor de un punto fijo llamado fulcro. Al aplicar una fuerza en un extremo de la palanca (fuerza de entrada), se genera un momento que permite levantar una carga en el otro extremo (fuerza de salida).
- Turbina de vapor: las turbinas de vapor que se utilizan en los generadores eléctricos de una central nuclear están diseñados para que el vapor genere una fuerza tangencial a la rueda y perpendicular al eje de forma que genere un momento de fuerzas para obtener un movimiento circular.
Polea: Una polea es una rueda con una cuerda o cable que la atraviesa. Al tirar de un extremo de la cuerda (fuerza de entrada), se aplica un momento sobre la Ejercicios resueltos
Ejercicio 1: Momento de una fuerza perpendicular al eje de rotación
Supongamos que tenemos una puerta que gira alrededor de sus bisagras, y aplicamos una fuerza de 20 newtons en la dirección perpendicular al eje de rotación, a una distancia de 0.5 metros desde el eje de rotación hasta el punto de aplicación de la fuerza. Calcula el momento de la fuerza.
Solución
El momento de la fuerza se calcularía de la siguiente manera:
Momento (τ) = F × r
τ = 20 N × 0.5 m
τ = 10 Nm
El momento de la fuerza aplicada sobre la puerta es de 10 newton metro (Nm).
Ejercicio 2: Momento de una fuerza no perpendicular al eje de rotación
Supongamos ahora que aplicamos una fuerza de 30 newtons sobre la misma puerta, pero esta vez la fuerza actúa en un ángulo de 60 grados respecto al eje de rotación, y la distancia desde el eje de rotación hasta el punto de aplicación de la fuerza es de 1 metro. Calcula el momento de la fuerza.
Solución
Para calcular el momento, primero debemos descomponer la fuerza en sus componentes perpendiculares al radio.
Fuerza perpendicular al radio (Fperpendicular) = F × cos(θ)
Fperpendicular = 30 N × cos(60°)
Fperpendicular = 30 N × 0.5
Fperpendicular = 15 N
Momento (τ) = Fperpendicular × r
τ = 15 N × 1 m
τ = 15 Nm
El momento de la fuerza aplicada sobre la puerta, considerando su componente perpendicular al radio, es de 15 newton metro (Nm).